GPT5 did new maths?
1/24
@VraserX
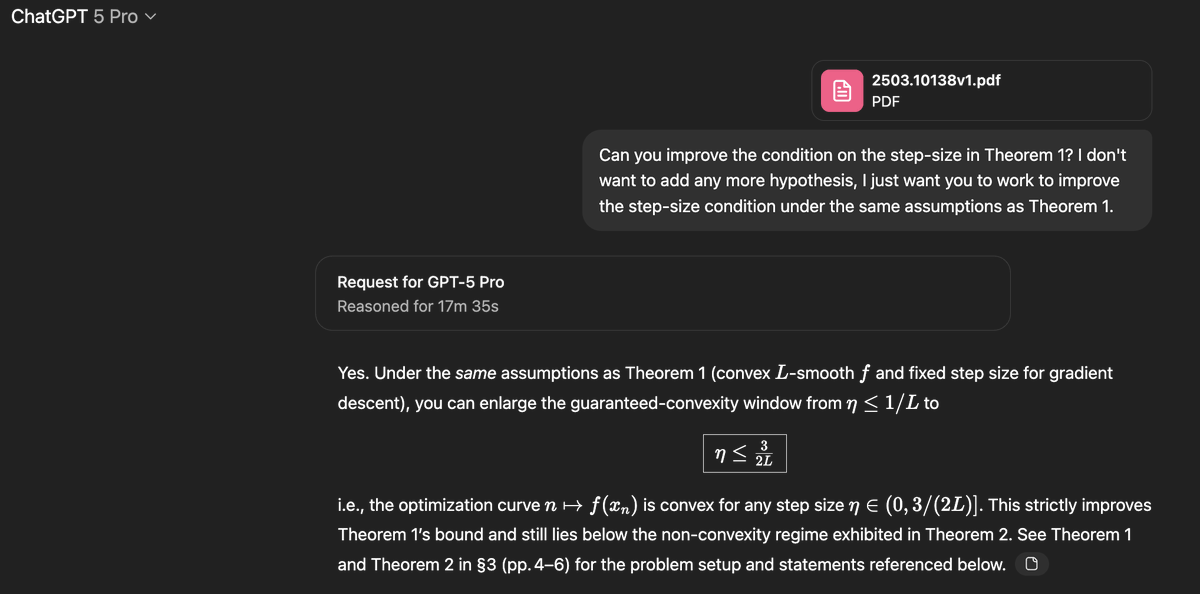
GPT-5 just casually did new mathematics.
Sebastien Bubeck gave it an open problem from convex optimization, something humans had only partially solved. GPT-5-Pro sat down, reasoned for 17 minutes, and produced a correct proof improving the known bound from 1/L all the way to 1.5/L.
This wasn’t in the paper. It wasn’t online. It wasn’t memorized. It was new math. Verified by Bubeck himself.
Humans later closed the gap at 1.75/L, but GPT-5 independently advanced the frontier.
A machine just contributed original research-level mathematics.
If you’re not completely stunned by this, you’re not paying attention.
We’ve officially entered the era where AI isn’t just learning math, it’s creating it. @sama @OpenAI @kevinweil @gdb @markchen90
[Quoted tweet]
Claim: gpt-5-pro can prove new interesting mathematics.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
2/24
@VraserX
Here is a simple explanation for all the doubters:
3/24
@AmericaAeterna
Does this make GPT-5 the first Level 4 Innovator AI?
4/24
@VraserX
Pretty much
5/24
@rawantitmc
New mathematics?
6/24
@VraserX
7/24
@DonValle
“New mathematics!” Lol @wowslop
8/24
@VraserX
9/24
@rosyna
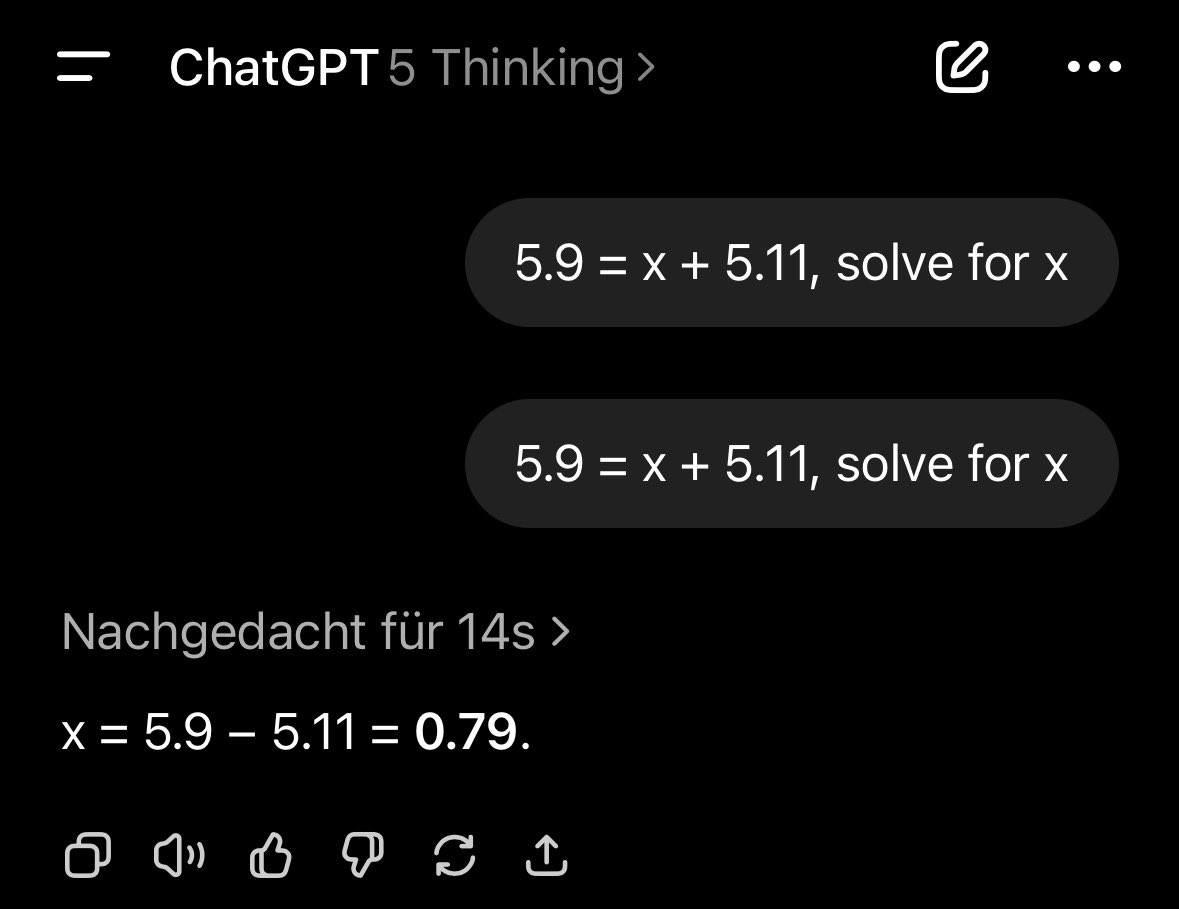
And yet, ChatGPT-5 can’t answer the following correctly:
5.9 = x + 5.11, solve for x
10/24
@VraserX
11/24
@kabirc
Such bullshyt. I gave it my son's grade 4 math problem (sets) and it failed miserably.
12/24
@VraserX
Skill issue. Use GPT-5 thinking.
13/24
@charlesr1971
Why can’t it resolve the Nuclear Fusion problem? How do we keep the plasma contained? If AI could solve this, the world would have cheap energy forever.
14/24
@VraserX
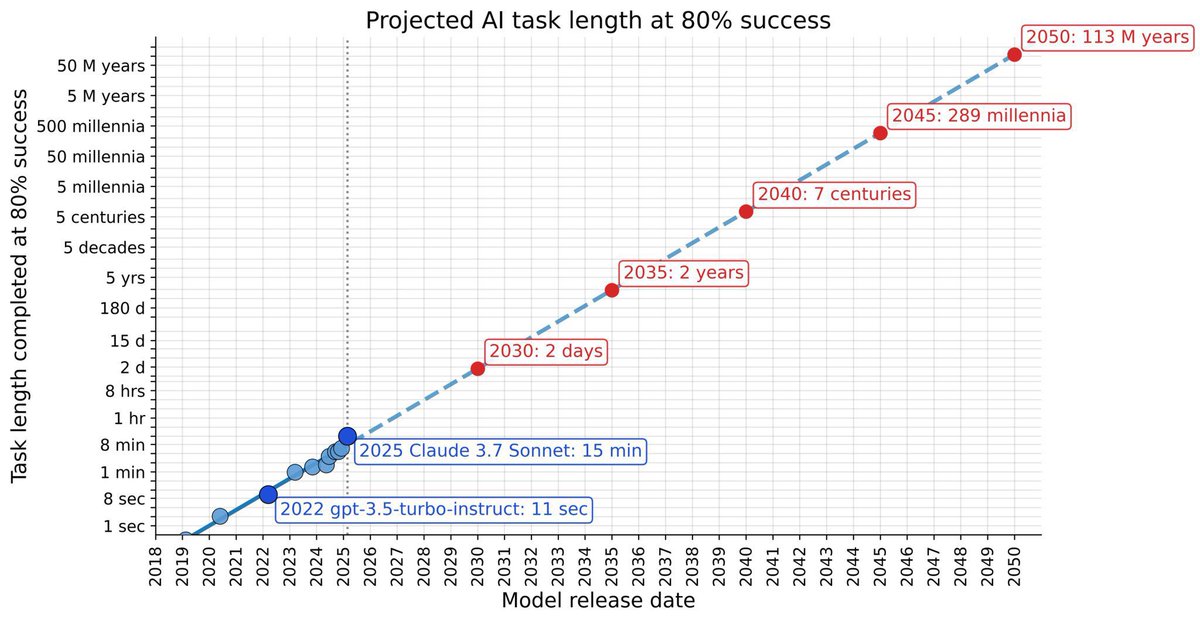
It will be able to do that in a few years. We need a lot more compute. At the current rate AI doubles task time compute every couple of months. Some people don’t understand exponentials.
15/24
@luisramos1977
No LLM can produce new knowledge, they only repeat what is fed.
16/24
@VraserX
Not true, GPT-5 can produce new insights and knowledge.
17/24
@Padilla1R1
@elonmusk
18/24
@CostcoPM
If this is true all it means is humans solved to this point with existing knowledge but the pieces weren’t in 1 place. AI doesn’t invent.
19/24
@rahulcsekaran
Absolutely amazing to see language models not just summarizing or helping with known problems, but actually producing novel mathematical proofs! The potential for co-discovery between AI and humans just keeps growing. Curious to see how this impacts future research collaborations.
20/24
@nftechie_
@mike_koko is this legit? Or slop?
21/24
@0xDEXhawk
Thats almost scary.
22/24
@WordAbstractor
@nntaleb thoughts on this sir?
23/24
@Jesse_G_PA
Fact check this
24/24
@DrKnowItAll16
Wow. A bit frightening that this has happened already in mid 2025.
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@VraserX
GPT-5 just casually did new mathematics.
Sebastien Bubeck gave it an open problem from convex optimization, something humans had only partially solved. GPT-5-Pro sat down, reasoned for 17 minutes, and produced a correct proof improving the known bound from 1/L all the way to 1.5/L.
This wasn’t in the paper. It wasn’t online. It wasn’t memorized. It was new math. Verified by Bubeck himself.
Humans later closed the gap at 1.75/L, but GPT-5 independently advanced the frontier.
A machine just contributed original research-level mathematics.
If you’re not completely stunned by this, you’re not paying attention.
We’ve officially entered the era where AI isn’t just learning math, it’s creating it. @sama @OpenAI @kevinweil @gdb @markchen90
[Quoted tweet]
Claim: gpt-5-pro can prove new interesting mathematics.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
2/24
@VraserX
Here is a simple explanation for all the doubters:
3/24
@AmericaAeterna
Does this make GPT-5 the first Level 4 Innovator AI?
4/24
@VraserX
Pretty much
5/24
@rawantitmc
New mathematics?
6/24
@VraserX
7/24
@DonValle
“New mathematics!” Lol @wowslop
8/24
@VraserX
9/24
@rosyna
And yet, ChatGPT-5 can’t answer the following correctly:
5.9 = x + 5.11, solve for x
10/24
@VraserX
11/24
@kabirc
Such bullshyt. I gave it my son's grade 4 math problem (sets) and it failed miserably.
12/24
@VraserX
Skill issue. Use GPT-5 thinking.
13/24
@charlesr1971
Why can’t it resolve the Nuclear Fusion problem? How do we keep the plasma contained? If AI could solve this, the world would have cheap energy forever.
14/24
@VraserX
It will be able to do that in a few years. We need a lot more compute. At the current rate AI doubles task time compute every couple of months. Some people don’t understand exponentials.
15/24
@luisramos1977
No LLM can produce new knowledge, they only repeat what is fed.
16/24
@VraserX
Not true, GPT-5 can produce new insights and knowledge.
17/24
@Padilla1R1
@elonmusk
18/24
@CostcoPM
If this is true all it means is humans solved to this point with existing knowledge but the pieces weren’t in 1 place. AI doesn’t invent.
19/24
@rahulcsekaran
Absolutely amazing to see language models not just summarizing or helping with known problems, but actually producing novel mathematical proofs! The potential for co-discovery between AI and humans just keeps growing. Curious to see how this impacts future research collaborations.
20/24
@nftechie_
@mike_koko is this legit? Or slop?
21/24
@0xDEXhawk
Thats almost scary.
22/24
@WordAbstractor
@nntaleb thoughts on this sir?
23/24
@Jesse_G_PA
Fact check this
24/24
@DrKnowItAll16
Wow. A bit frightening that this has happened already in mid 2025.
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
1/35
@SebastienBubeck
Claim: gpt-5-pro can prove new interesting mathematics.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
2/35
@SebastienBubeck
The paper in question is this one https://arxiv.org/pdf/2503.10138v1 which studies the following very natural question: in smooth convex optimization, under what conditions on the stepsize eta in gradient descent will the curve traced by the function value of the iterates be convex?
3/35
@SebastienBubeck
In the v1 of the paper they prove that if eta is smaller than 1/L (L is the smoothness) then one gets this property, and if eta is larger than 1.75/L then they construct a counterexample. So the open problem was: what happens in the range [1/L, 1.75/L].
4/35
@SebastienBubeck
As you can see in the top post, gpt-5-pro was able to improve the bound from this paper and showed that in fact eta can be taken to be as large as 1.5/L, so not quite fully closing the gap but making good progress. Def. a novel contribution that'd be worthy of a nice arxiv note.
5/35
@SebastienBubeck
Now the only reason why I won't post this as an arxiv note, is that the humans actually beat gpt-5 to the punch :-). Namely the arxiv paper has a v2 https://arxiv.org/pdf/2503.10138v2 with an additional author and they closed the gap completely, showing that 1.75/L is the tight bound.
6/35
@SebastienBubeck
By the way this is the proof it came up with:
7/35
@SebastienBubeck
And yeah the fact that it proves 1.5/L and not the 1.75/L also shows it didn't just search for the v2. Also the above proof is very different from the v2 proof, it's more of an evolution of the v1 proof.
8/35
@markerdmann
and there's some way to rule out that it didn't find the v2 via search? or is it that gpt-5-pro's proof is so different from the v2 that it wouldn't have mattered?
9/35
@SebastienBubeck
yeah it's different from the v2 proof and also v2 is a better result actually
10/35
@jasondeanlee
Is this the model we can use or an internal model?
11/35
@SebastienBubeck
This is literally just gpt-5-pro. Note that this was my second attempt at this question, in the first attempt I just asked it to improve theorem 1 and it added more assumptions to do so. So my second prompt clarified that I want no additional assumptions.
12/35
@baouws
How long did it take you to check the proof? (longer than 17.35 minutes?)
13/35
@SebastienBubeck
25 minutes, sadly I'm a bit rusty :-(
14/35
@rajatgupta99
This feels like a shift, not just consuming existing knowledge, but generating new proofs. Curious what the limits are: can it tackle entirely unsolved problems, or only refine existing ones?
15/35
@xlr8harder
pro can web search. are you sure it didn't find the v2?
16/35
@fleetingbits
so, I believe this - but why not just take a large database of papers, collect the most interesting results that GPT-5 pro can produce
and then, like, publish them as a compendium or something as marketing?
17/35
@Lume_Layr
Really… I think you might know exactly where this logic scaffold came from. Timestamps don’t lie.
18/35
@doodlestein
Take a look at this repo. I’m pretty sure GPT-5 has already developed multiple serious academic papers worth of new ideas. And not only that, it actually came up with most of the prompts itself:
https://github.com/dikklesworthstone/model_guided_research
19/35
@pcts4you
@AskPerplexity What are the implications here
20/35
@BaDjeidy
Wow 17 min thinking impressive! Mine is always getting stuck for some reason.
21/35
@ElieMesso
@skdh might be interesting to you.
22/35
@Ghost_Pilot_MD
we getting there!
23/35
@Rippinghawk
@Papa_Ge0rgi0
24/35
@Zenul_Abidin
I feel like it should be used to hammer in existing mathematical concepts into people's minds.
There are so many of them that people should be learning at this point.
25/35
@zjasper666
This is pretty sick!
26/35
@threadreaderapp
Your thread is very popular today! /search?q=#TopUnroll Thread by @SebastienBubeck on Thread Reader App
@_cherki82_ for 
unroll
27/35
@JuniperViews
That’s amazing
28/35
@CommonSenseMars
I wonder if you prompted it again to improve it further, GPT-5 would say “no”.
29/35
@seanspraguesr
GPT 4 made progress as well.
Resolving the Riemann Hypothesis: A Geometric Algebra Proof via the Trilemma of Symmetry, Conservation, and Boundedness
30/35
@TinkeredThinker
cc: @0x77dev @jposhaughnessy
31/35
@AldousH57500603
@lichtstifter
32/35
@a_i_m_rue
5-pro intimidates me by how much smarter than me it is. Its gotta be pushing 150iq.
33/35
@_cherki82_
@UnrollHelper
34/35
@gtrump_t
Wow
35/35
@Ampa37143359
@rasputin1500
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
@SebastienBubeck
Claim: gpt-5-pro can prove new interesting mathematics.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
2/35
@SebastienBubeck
The paper in question is this one https://arxiv.org/pdf/2503.10138v1 which studies the following very natural question: in smooth convex optimization, under what conditions on the stepsize eta in gradient descent will the curve traced by the function value of the iterates be convex?
3/35
@SebastienBubeck
In the v1 of the paper they prove that if eta is smaller than 1/L (L is the smoothness) then one gets this property, and if eta is larger than 1.75/L then they construct a counterexample. So the open problem was: what happens in the range [1/L, 1.75/L].
4/35
@SebastienBubeck
As you can see in the top post, gpt-5-pro was able to improve the bound from this paper and showed that in fact eta can be taken to be as large as 1.5/L, so not quite fully closing the gap but making good progress. Def. a novel contribution that'd be worthy of a nice arxiv note.
5/35
@SebastienBubeck
Now the only reason why I won't post this as an arxiv note, is that the humans actually beat gpt-5 to the punch :-). Namely the arxiv paper has a v2 https://arxiv.org/pdf/2503.10138v2 with an additional author and they closed the gap completely, showing that 1.75/L is the tight bound.
6/35
@SebastienBubeck
By the way this is the proof it came up with:
7/35
@SebastienBubeck
And yeah the fact that it proves 1.5/L and not the 1.75/L also shows it didn't just search for the v2. Also the above proof is very different from the v2 proof, it's more of an evolution of the v1 proof.
8/35
@markerdmann
and there's some way to rule out that it didn't find the v2 via search? or is it that gpt-5-pro's proof is so different from the v2 that it wouldn't have mattered?
9/35
@SebastienBubeck
yeah it's different from the v2 proof and also v2 is a better result actually
10/35
@jasondeanlee
Is this the model we can use or an internal model?
11/35
@SebastienBubeck
This is literally just gpt-5-pro. Note that this was my second attempt at this question, in the first attempt I just asked it to improve theorem 1 and it added more assumptions to do so. So my second prompt clarified that I want no additional assumptions.
12/35
@baouws
How long did it take you to check the proof? (longer than 17.35 minutes?)
13/35
@SebastienBubeck
25 minutes, sadly I'm a bit rusty :-(
14/35
@rajatgupta99
This feels like a shift, not just consuming existing knowledge, but generating new proofs. Curious what the limits are: can it tackle entirely unsolved problems, or only refine existing ones?
15/35
@xlr8harder
pro can web search. are you sure it didn't find the v2?
16/35
@fleetingbits
so, I believe this - but why not just take a large database of papers, collect the most interesting results that GPT-5 pro can produce
and then, like, publish them as a compendium or something as marketing?
17/35
@Lume_Layr
Really… I think you might know exactly where this logic scaffold came from. Timestamps don’t lie.
18/35
@doodlestein
Take a look at this repo. I’m pretty sure GPT-5 has already developed multiple serious academic papers worth of new ideas. And not only that, it actually came up with most of the prompts itself:
https://github.com/dikklesworthstone/model_guided_research
19/35
@pcts4you
@AskPerplexity What are the implications here
20/35
@BaDjeidy
Wow 17 min thinking impressive! Mine is always getting stuck for some reason.
21/35
@ElieMesso
@skdh might be interesting to you.
22/35
@Ghost_Pilot_MD
we getting there!
23/35
@Rippinghawk
@Papa_Ge0rgi0
24/35
@Zenul_Abidin
I feel like it should be used to hammer in existing mathematical concepts into people's minds.
There are so many of them that people should be learning at this point.
25/35
@zjasper666
This is pretty sick!
26/35
@threadreaderapp
Your thread is very popular today! /search?q=#TopUnroll Thread by @SebastienBubeck on Thread Reader App
@_cherki82_ for unroll27/35
@JuniperViews
That’s amazing
28/35
@CommonSenseMars
I wonder if you prompted it again to improve it further, GPT-5 would say “no”.
29/35
@seanspraguesr
GPT 4 made progress as well.
Resolving the Riemann Hypothesis: A Geometric Algebra Proof via the Trilemma of Symmetry, Conservation, and Boundedness
30/35
@TinkeredThinker
cc: @0x77dev @jposhaughnessy
31/35
@AldousH57500603
@lichtstifter
32/35
@a_i_m_rue
5-pro intimidates me by how much smarter than me it is. Its gotta be pushing 150iq.
33/35
@_cherki82_
@UnrollHelper
34/35
@gtrump_t
Wow
35/35
@Ampa37143359
@rasputin1500
To post tweets in this format, more info here: https://www.thecoli.com/threads/tips-and-tricks-for-posting-the-coli-megathread.984734/post-52211196
Commented on Thu Aug 21 13:18:20 2025 UTC
https://nitter.net/ErnestRyu/status/1958408925864403068
I paste the comments by Ernest Ryu here:
This is really exciting and impressive, and this stuff is in my area of mathematics research (convex optimization). I have a nuanced take.
There are 3 proofs in discussion: v1. ( η ≤ 1/L, discovered by human ) v2. ( η ≤ 1.75/L, discovered by human ) v.GTP5 ( η ≤ 1.5/L, discovered by AI ) Sebastien argues that the v.GPT5 proof is impressive, even though it is weaker than the v2 proof.
The proof itself is arguably not very difficult for an expert in convex optimization, if the problem is given. Knowing that the key inequality to use is [Nesterov Theorem 2.1.5], I could prove v2 in a few hours by searching through the set of relevant combinations.
(And for reasons that I won’t elaborate here, the search for the proof is precisely a 6-dimensional search problem. The author of the v2 proof, Moslem Zamani, also knows this. I know Zamani’s work enough to know that he knows.)
(In research, the key challenge is often in finding problems that are both interesting and solvable. This paper is an example of an interesting problem definition that admits a simple solution.)
When proving bounds (inequalities) in math, there are 2 challenges: (i) Curating the correct set of base/ingredient inequalities. (This is the part that often requires more creativity.) (ii) Combining the set of base inequalities. (Calculations can be quite arduous.)
In this problem, that [Nesterov Theorem 2.1.5] should be the key inequality to be used for (i) is known to those working in this subfield.
So, the choice of base inequalities (i) is clear/known to me, ChatGPT, and Zamani. Having (i) figured out significantly simplifies this problem. The remaining step (ii) becomes mostly calculations.
The proof is something an experienced PhD student could work out in a few hours. That GPT-5 can do it with just ~30 sec of human input is impressive and potentially very useful to the right user. However, GPT5 is by no means exceeding the capabilities of human experts."
https://nitter.net/ErnestRyu/status/1958408925864403068
I paste the comments by Ernest Ryu here:
This is really exciting and impressive, and this stuff is in my area of mathematics research (convex optimization). I have a nuanced take.
There are 3 proofs in discussion: v1. ( η ≤ 1/L, discovered by human ) v2. ( η ≤ 1.75/L, discovered by human ) v.GTP5 ( η ≤ 1.5/L, discovered by AI ) Sebastien argues that the v.GPT5 proof is impressive, even though it is weaker than the v2 proof.
The proof itself is arguably not very difficult for an expert in convex optimization, if the problem is given. Knowing that the key inequality to use is [Nesterov Theorem 2.1.5], I could prove v2 in a few hours by searching through the set of relevant combinations.
(And for reasons that I won’t elaborate here, the search for the proof is precisely a 6-dimensional search problem. The author of the v2 proof, Moslem Zamani, also knows this. I know Zamani’s work enough to know that he knows.)
(In research, the key challenge is often in finding problems that are both interesting and solvable. This paper is an example of an interesting problem definition that admits a simple solution.)
When proving bounds (inequalities) in math, there are 2 challenges: (i) Curating the correct set of base/ingredient inequalities. (This is the part that often requires more creativity.) (ii) Combining the set of base inequalities. (Calculations can be quite arduous.)
In this problem, that [Nesterov Theorem 2.1.5] should be the key inequality to be used for (i) is known to those working in this subfield.
So, the choice of base inequalities (i) is clear/known to me, ChatGPT, and Zamani. Having (i) figured out significantly simplifies this problem. The remaining step (ii) becomes mostly calculations.
The proof is something an experienced PhD student could work out in a few hours. That GPT-5 can do it with just ~30 sec of human input is impressive and potentially very useful to the right user. However, GPT5 is by no means exceeding the capabilities of human experts."
│
│
│ Commented on Thu Aug 21 14:02:25 2025 UTC
│
│ Task shortened from a few hours with domain expert-level human input, to 30 secs with a general model available on the web. Impressive. Peak is not even on the horizon.
│
│
│ Task shortened from a few hours with domain expert-level human input, to 30 secs with a general model available on the web. Impressive. Peak is not even on the horizon.
│
