Godel's Incompleteness Theorem

[SkillClash]

Kurt Godel was by far the greatest logician of all time

this shyt is insane

"Any effectivelly generated theory capable of expressing elementary arithmetic cannot be both consistent and complete"



so does this mean that we can never find consistency in mathematics, science etc.

 

[SkillClash]

shyt raw

 

[blackzeus]

Kurt Godel was by far the greatest logician of all time

this shyt is insane

"Any effectivelly generated theory capable of expressing elementary arithmetic cannot be both consistent and complete"



so does this mean that we can never find consistency in mathematics, science etc.

1+1 is not consistent and complete? It relates more to computer programming:

E.g. N*(n-1) You have to prove both the negation and the statement for the theory to be consistent and complete. So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false. But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n+1) is not equal to 0 until you can prove it. Basically a lot of sh*t in math is taken for granted, especially in recursive sets of elements, basically a function playing on itself. In short, even scientists operate on faith sometimes

 

[SkillClash]

1+1 is not consistent and complete? It relates more to computer programming:

E.g. N*(n-1) You have to prove both the negation and the statement for the theory to be consistent and complete. So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false. But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it. Basically a lot of sh*t is math is taken for granted, especially in recursive sets of elements, basically a function playing on itself. In short, even scientists operate on faith sometimes

you a mathematician?

 

[blackzeus]

you a mathematician?

Ain't I?

 

[SkillClash]

Ain't I?

are you in academia? a student or just a self-taught mathematician

 

[blackzeus]

are you in academia? a student or just a self-taught mathematician

I'm overseas right now breh, but yeah I went to school What's your point? You don't know any brothers who know math cuzzo?

 

[☑︎#VoteDemocrat]

1+1 is not consistent and complete? It relates more to computer programming:

E.g. N*(n-1) You have to prove both the negation and the statement for the theory to be consistent and complete. So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false. But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it. Basically a lot of sh*t is math is taken for granted, especially in recursive sets of elements, basically a function playing on itself. In short, even scientists operate on faith sometimes

problem of induction

+

Nihilism

=

 

[DANKTHRONE]

1+1 is not consistent and complete? It relates more to computer programming:

E.g. N*(n-1) You have to prove both the negation and the statement for the theory to be consistent and complete. So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false. But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it. Basically a lot of sh*t is math is taken for granted, especially in recursive sets of elements, basically a function playing on itself. In short, even scientists operate on faith sometimes

All of this is wrong

 

[blackzeus]

All of this is wrong

OK breh, let's hear your point of view, we're all here to build

 

[DANKTHRONE]

1+1 is not consistent and complete?

It doesn't make sense to ask if 1+1 is complete and consistent. You have to ask that about axiomatic systems. And a system that is as strong as Peano Arithmetic isn't.

You have to prove both the negation and the statement for the theory to be consistent and complete.

If you are using the law of the excluded middle, then you only have to show one or the other.

So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false.

Again, there is no need to prove both of those statements. If you know J is true, then ~J is necessarily false.

But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it

With Mathematical induction you can show that statements hold true for infinite sets.

 

[blackzeus]

1+1 is not consistent and complete?

It doesn't make sense to ask if 1+1 is complete and consistent. You have to ask that about axiomatic systems. And a system that is as strong as Peano Arithmetic isn't.

You have to prove both the negation and the statement for the theory to be consistent and complete.

If you are using the law of the excluded middle, then you only have to show one or the other.

So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false.

Again, there is no need to prove both of those statements. If you know J is true, then ~J is necessarily false.

But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it

With Mathematical induction you can show that statements hold true for infinite sets.

1) The 1+1 example was in reply to OPs post. Basically at the micro scale of things Godel's theorem is not true. Otherwise we would be on some does chicken taste like chicken type conversation. I said computer programming because that's exactly where a lot of these issues come up. Here actually is a wiki link to Hilbert's program, of which its goal was to provide axiomatic solutions to all math:

Hilbert's Program Wiki

In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies. As a solution, Hilbert proposed to ground all existing theories to a finite, complete set of axioms, and provide a proof that these axioms were consistent. Hilbert proposed that the consistency of more complicated systems, such as real analysis, could be proven in terms of simpler systems. Ultimately, the consistency of all of mathematics could be reduced to basic arithmetic.

In essence, you should be able to solve the complex by breaking everything down into its basic integers, which is the basis of binary logic, aka computer programming/machine language. The issue with that is that you can't even consistently and completely prove integers, AKA Peano arithmetic. So basically, you can't use the scientific principle for a lot of math, you have to BELIEVE certain things are true. That's when I got into the examples with the inverse hyperbola. We don't really know what exists at infinity, but the logical assumption is that it trends towards 0.<<<<<<-------To be a scientist/mathematician and talk about logical assumptions is intrinsically crazy, which is what Godel's point basically is, the irony that we can't technically prove everything math is built on in an infinite recursive set. Sure over a subset our axioms are correct, but that's where it begins and ends. I don't agree with your insinuation that mathematical induction is consistent and complete proof. Consistent and complete proof is A) What I say is true for everything I say and B) The exact opposite of what I say is always false. That's what I got from it But to your point of view as well, feels good to talk to brothers with brains

 

[Mission249]

"Any effectivelly generated theory capable of expressing elementary arithmetic cannot be both consistent and complete"

1+1 is not consistent and complete?

"1+1" (==2?) is not an "effectively generated theory capable of expressing elementary arithmetic". It is a statement within a system of axioms, Paeno Arithmetic.

Basically at the micro scale of things Godel's theorem is not true.

It's true at every "scale" you just accidentally switched up what he was talking about.

The issue with that is that you can't even consistently and completely prove integers, AKA Peano arithmetic.

Yes, you can. The 2nd incompleteness theorem says Paeno arithmetic can't prove itself; however, a stronger model can (i.e. http://en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory). ZFC can't prove itself; however a stronger model can, and so on. All of these systems of axioms start to break down and not make sense when they become self-referential (e.g. in English saying: "this statement is not true"). From my cursory googling, Paeno arithmetic becomes self-referential with multiplication (i.e. multiplication is just a number plus itself a certain number of times), but I'm not sure on that.

So basically, you can't use the scientific principle for a lot of math, you have to BELIEVE certain things are true ... I don't agree with your insinuation that mathematical induction is consistent and complete proof.

I think your mixing up mathematical induction and scientific method induction. While, yes, the scientific method's induction is somewhat of a "leap of faith" (an incredibly small one), mathematical induction is not. We made the rules of the mathematical system and Godel is just pointing out that our system will have some statements that are undecidable. When we throw a ball into the air and theorize that "what must go up always comes down", we back that with centuries of experiments and deduction, but we're never 100% sure (see: http://en.wikipedia.org/wiki/Black_swan_theory). When we say the sum of infinite series A == finite number B, we know that's a fact within our mathematical system even tho the statements deals with infinite numbers. It isn't a leap of faith in the slightest.

feels good to talk to brothers with brains

Yes it does

 

[714562]

Really is amazing how much boils down to "trust what you repeatedly observe." even in modern science and mathematics

 

[blackzeus]

"1+1" (==2?) is not an "effectively generated theory capable of expressing elementary arithmetic". It is a statement within a system of axioms, Paeno Arithmetic.

I don't want to argue over definitions, but a statement is a subset of an axiom. E.g., if I say x+y = y+x, then 1+2 = 3 = 2+1 is a subset of that axiom, e.g. a mathematical relation that follows said axiom, but that's not the main point here IMHO>

It's true at every "scale" you just accidentally switched up what he was talking about.

Godell's theorem is not true for all subsets of axiomatic theory, even if you want to choose natural numbers for example, when is x = x not consistently and completely true?

Yes, you can. The 2nd incompleteness theorem says Paeno arithmetic can't prove itself; however, a stronger model can (i.e. http://en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory). ZFC can't prove itself; however a stronger model can, and so on. All of these systems of axioms start to break down and not make sense when they become self-referential (e.g. in English saying: "this statement is not true"). From my cursory googling, Paeno arithmetic becomes self-referential with multiplication (i.e. multiplication is just a number plus itself a certain number of times), but I'm not sure on that.

Self-referential = recursive, which is what I mentioned in my first post. The physical example I gave of an inverse hyperbola shows that it is supposed to trend towards 0 but that is something we ASSUME. You can't consistently and completely prove that at infinity x = 0 because THERE IS NO PHYSICAL QUANTIFICATION OF INFINITY. Infinity is a concept, not a numerical fact. That's the inherent limitation! Every time you use calculus or differential equations you ASSUME certain things to be true in order to solve your problem. Thus, in all but the most trivial axiomatic systems (e.g. addition), you can't consistently and completely prove everything, you have to make ASSUMPTIONS (e.g. limits). All recursive functions that trend towards a value must trend towards either infinity or 0. (using cartesian coordinate system) So we assume that eventually it reaches 0 or infinity in order to simplify our lives. We know it to be true becaue it works out in our calculations, but we can't consistently and completely prove it. Feel free to correct me if you feel I'm wrong.

I think your mixing up mathematical induction and scientific method induction. While, yes, the scientific method's induction is somewhat of a "leap of faith" (an incredibly small one), mathematical induction is not. We made the rules of the mathematical system and Godel is just pointing out that our system will have some statements that are undecidable. When we throw a ball into the air and theorize that "what must go up always comes down", we back that with centuries of experiments and deduction, but we're never 100% sure (see: http://en.wikipedia.org/wiki/Black_swan_theory). When we say the sum of infinite series A == finite number B, we know that's a fact within our mathematical system even tho the statements deals with infinite numbers. It isn't a leap of faith in the slightest.

What is mathematical induction? You have:

1) Base case. E.g. 0+1+2+3+...= (n*(n+1))/2

2) Induction step. Let's declare a set G(n) for all natural numbers. If G(n) is true, then G(n+1) is also true. Using quadratics you can prove that in fact it is also true for G(n+1) as follows:

(0+1+2+..)+(n+1)=((n+1)*((n+1)+1))/2

Now remember for induction we ASSUME (big key word, how in the f*ck is that not a leap of faith?!! ) the base case is true, so assuming in fact 0+1+2+3+...= (n*(n+1))/2 is true, we get---->

1)...=(n*(n+1))/2 + (n+1) = ((n+1)*((n+1)+1))/2

2)...((n+1)*((n+1)+1))/2 = (n*(n+1)+(n+1)+(n+1))/2 = (n*(n+1)+2(n+1))/2 (I did that by multiplying the numerator, stay with me now)

3)... (n*(n+1)+2(n+1))/2 = (n^2+n+2n+2)/2 (oh wow, quadratics!, using quadratics in the numerator...

4)...(n^2+n+2n+2)/2= (n+1)*(n+2)/2 (oh wow, I think I see it!)....

5)...(n+1)*(n+2)/2 =((n+1)*((n+1)+1))/2 (yeah, I proved it!!!!! )



All good right? WRONG!!!

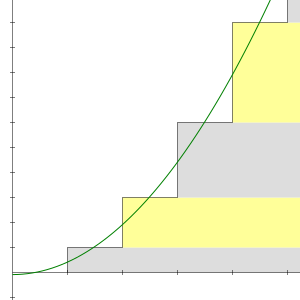
^^^This is the chart using cartesian coordinates for the above proof via induction. In fact, the summation formula proved via induction is DIVERGENT, it does not approach a finite limit, so in reality the induction proof is not true for the ENTIRE subset. This is what Godell is getting at. How the hell does infinity = infinity^2/2? So again how is mathematical induction consistent AND complete proof? Matter of fact, how can ANYTHING that involves an assumption as a foundation lead to consistent and complete proof at all? You don't see the irony in that? That's what Godell saw! If it wasn't true, you would never get error messages on your calculator. It does so because it has inherent limitations. So in fact, in science as well you must use faith to get by, because you can't REALLY prove everything to be true, you just know it is.

Yes it does