OCCAMS_RAZOR
Pro
@blackzeus do you know a lot about algorithm analysis? i may need your help with a proof i have to do for an assignment.
Godel's Incompleteness Theorem
- Thread starter SkillClash
- Start date
I don't want to argue over definitions, but a statement is a subset of an axiom. E.g., if I say x+y = y+x, then 1+2 = 3 = 2+1 is a subset of that axiom, e.g. a mathematical relation that follows said axiom, but that's not the main point here IMHO>
Godell's theorem is not true for all subsets of axiomatic theory, even if you want to choose natural numbers for example, when is x = x not consistently and completely true?
Self-referential = recursive, which is what I mentioned in my first post. The physical example I gave of an inverse hyperbola shows that it is supposed to trend towards 0 but that is something we ASSUME. You can't consistently and completely prove that at infinity x = 0 because THERE IS NO PHYSICAL QUANTIFICATION OF INFINITY. Infinity is a concept, not a numerical fact. That's the inherent limitation! Every time you use calculus or differential equations you ASSUME certain things to be true in order to solve your problem. Thus, in all but the most trivial axiomatic systems (e.g. addition), you can't consistently and completely prove everything, you have to make ASSUMPTIONS (e.g. limits). All recursive functions that trend towards a value most trend towards either infinity or 0. (using cartesian coordinate system) So we assume that eventually it reaches 0 or infinity in order to simplify our lives. We know it to be true becaue it works out in our calculations, but we can't consistently and completely prove it. Feel free to correct me if you feel I'm wrong.
What is mathematical induction? You have:
1) Base case. E.g. 0+1+2+3+...= (n*(n+1))/2
2) Induction step. Let's declare a set G(n) for all natural numbers. If G(n) is true, then G(n+1) is also true. Using quadratics you can prove that in fact it is also true for G(n+1) as follows:
(0+1+2+..)+(n+1)=((n+1)*((n+1)+1))/2
Now remember for induction we ASSUME (big key word, how in the f*ck is that not a leap of faith?!!) the base case is true, so assuming in fact 0+1+2+3+...= (n*(n+1))/2 is true, we get---->
1)...=(n*(n+1))/2 + (n+1) = ((n+1)*((n+1)+1))/2
2)...((n+1)*((n+1)+1))/2 = (n*(n+1)+(n+1)+(n+1))/2 = (n*(n+1)+2(n+1))/2 (I did that by multiplying the numerator, stay with me now)
3)... (n*(n+1)+2(n+1))/2 = (n^2+n+2n+2)/2 (oh wow, quadratics!, using quadratics in the numerator...
4)...(n^2+n+2n+2)/2= (n+1)*(n+2)/2 (oh wow, I think I see it!)....
5)...(n+1)*(n+2)/2 =((n+1)*((n+1)+1))/2 (yeah, I proved it!!!!!)
All good right?WRONG!!!
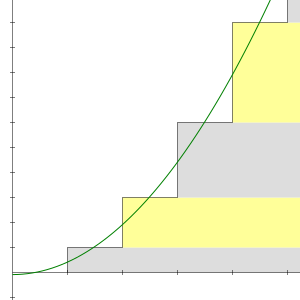
^^^This is the chart using cartesian coordinates for the above proof via induction. In fact, the summation formula proved via induction is DIVERGENT, it does not approach a finite limit, so in reality the induction proof is not true for the ENTIRE subset. This is what Godell is getting at. How the hell does infinity = infinity^2/2?
So again how is mathematical induction consistent AND complete proof?
Matter of fact, how can ANYTHING that involves an assumption as a foundation lead to consistent and complete proof at all? You don't see the irony in that? That's what Godell saw! If it wasn't true, you would never get error messages on your calculator. It does so because it has inherent limitations. So in fact, in science as well you must use faith to get by, because you can't REALLY prove everything to be true, you just know it is.
what you demonstrated here is misunderstanding in proof of by induction rather than a problem with the method. you can't assume 0+1+2+3+...= (n*(n+1))/2. when you do that you assume that your statement is true and there is noting left to prove.
No, that's wrong, you're mistaking assumption aka faith for science. That's why it's called "induction", and not "consistent and complete". You prove it's true for an element in the set you're using for your axiom. then you say, since it holds for element #1, let's assume it holds for element n. Induction ALWAYS involves that leap of faith. Using my example above, 0 = (0*(0+1))/2. so the statement is true for element 0. Then based on that, let's assume it's true for n,....and you know the rest. that's why the proof works but in reality the axiom is false over the entire set of natural numbers. Most proofs involve assumptions aka faith at one point or another, it is blowing my mind that y'all not getting what Godell is saying. He is simply saying since most of your proofs outside of basic mathematical operations involve assumptions, ESPECIALLY in recursive sets/axioms, you can't consistently and completely prove the majority of what you state is true! Faith and science have become one!
Last edited:
Y'all need to get to the background of what is going on here, for a deeper understanding, y'all missin' the point like the Miami Heat. Here is a wiki link on Godel:
http://en.wikipedia.org/wiki/Kurt_Gödel#Religious_views
Y'all not realizing that Godel just shat on modern math with his theory. All the major scientists of his era (and let's be real, the 30-50s was the last TRUE era of advancement in scientific theory) were saying evolution this and God doesn't exist that, and faith is b.s. bla bla bla. Godel was like, "O rly?
let's have a look see at the basis of your great math, natural numbers. Well I can't believe it, these numbers ain't loyal!
Can I join your religion of math?"
http://en.wikipedia.org/wiki/Kurt_Gödel#Religious_views
Y'all not realizing that Godel just shat on modern math with his theory. All the major scientists of his era (and let's be real, the 30-50s was the last TRUE era of advancement in scientific theory) were saying evolution this and God doesn't exist that, and faith is b.s. bla bla bla. Godel was like, "O rly?
let's have a look see at the basis of your great math, natural numbers. Well I can't believe it, these numbers ain't loyal!
Last edited:
No, that's wrong, you're mistaking assumption aka faith for science. That's why it's called "induction", and not "consistent and complete". You prove it's true for an element in the set you're using for your axiom. then you say, since it holds for element #1, let's assume it holds for element n. Induction ALWAYS involves that leap of faith. Using my example above, 0 = (0*(0+1))/2. so the statement is true for element 0. Then based on that, let's assume it's true for n,....and you know the rest. that's why the proof works but in reality the axiom is false over the entire subset of natural numbers. Most proofs involve assumptions aka faith at one point or another, it is blowing my mind that y'all not getting what Godell is saying. He is simply saying since most of your proofs outside of basic mathematical operations involve assumptions, ESPECIALLY in recursive sets/axioms, you can't consistently and completely prove the majority of what you state is true! Faith and science have become one!
yes and after you take that leap of faith the next step is to see whether it's true or not. you just don't stick with the leap of and say QED. and as far as your example i don't see how it disproves anything. if by the step where you claimed you proved it the right hand side is not equal to you the left hand side then you having proved anything if it is then they would hold for all natural numbers.
So does infinity = infinity^2/2?
Is not the proof correct but the statement divergent using the set of all natural numbers? Is this in what you place your beliefs?
Last edited:
So does infinity = infinity^2/2?Again, please advise me the steps required to join the faith you call mathGodell trolled y'all scientists and you not even realizing it
what statement is divergent and so what if it is. and what is infinity?
It's been years playboy I'm a bit rusty, you're probably better off with a classmate but why not? It's good to keep my brain fresh.
Please reread my post breh. You missed the point like the Chicago Bulls:
Self-referential = recursive, which is what I mentioned in my first post. The physical example I gave of an inverse hyperbola shows that it is supposed to trend towards 0 but that is something we ASSUME. You can't consistently and completely prove that at infinity x = 0 because THERE IS NO PHYSICAL QUANTIFICATION OF INFINITY. Infinity is a concept, not a numerical fact. That's the inherent limitation! Every time you use calculus or differential equations you ASSUME certain things to be true in order to solve your problem. Thus, in all but the most trivial axiomatic systems (e.g. addition), you can't consistently and completely prove everything, you have to make ASSUMPTIONS (e.g. limits). All recursive functions that trend towards a value most trend towards either infinity or 0. (using cartesian coordinate system) So we assume that eventually it reaches 0 or infinity in order to simplify our lives. We know it to be true becaue it works out in our calculations, but we can't consistently and completely prove it. Feel free to correct me if you feel I'm wrong.
What is mathematical induction? You have:
1) Base case. E.g. 0+1+2+3+...= (n*(n+1))/2
2) Induction step. Let's declare a set G(n) for all natural numbers. If G(n) is true, then G(n+1) is also true. Using quadratics you can prove that in fact it is also true for G(n+1) as follows:
(0+1+2+..)+(n+1)=((n+1)*((n+1)+1))/2
Now remember for induction we ASSUME (big key word, how in the f*ck is that not a leap of faith?!!
1)...=(n*(n+1))/2 + (n+1) = ((n+1)*((n+1)+1))/2
2)...((n+1)*((n+1)+1))/2 = (n*(n+1)+(n+1)+(n+1))/2 = (n*(n+1)+2(n+1))/2 (I did that by multiplying the numerator, stay with me now)
3)... (n*(n+1)+2(n+1))/2 = (n^2+n+2n+2)/2 (oh wow, quadratics!, using quadratics in the numerator...
4)...(n^2+n+2n+2)/2= (n+1)*(n+2)/2 (oh wow, I think I see it!)....
5)...(n+1)*(n+2)/2 =((n+1)*((n+1)+1))/2 (yeah, I proved it!!!!!
All good right?
^^^This is the chart using cartesian coordinates for the above proof via induction. In fact, the summation formula proved via induction is DIVERGENT, it does not approach a finite limit, so in reality the induction proof is not true for the ENTIRE subset. This is what Godell is getting at. How the hell does infinity = infinity^2/2?
i've been saying this for years. but nobody listens. all that stuff about we know this we know that. we REALLLLY dont know nothing. WE ASSUME things based on the patters we can see currently and have seen in the past(once we were able to locate information of the past). some things that happened to far back where we have no written evidence of someone else counting. we have to ASSUME/Guess to some degree or take an educated guess. by stretching a pattern we do see today out to cover for what we dont see in history and in the future.1+1 is not consistent and complete? It relates more to computer programming:
E.g. N*(n-1) You have to prove both the negation and the statement for the theory to be consistent and complete. So for example if you say according to your theory from Set (0,infinity) N*(n-1) = 0, you have to prove it is both true for every element of the set, and that also the contrary is false. But you have to realize that in a lot of these theories in our reality you have to make an approximation, e.g. inverse hyperbola that approaches +/- infinity. Theoretically you assume that it approaches infinity, but in your lifetime you will never be able to prove that, there's too many elements to the set. You can't discount the fact that perhaps at infinity, N*(n1) is not equal to 0 until you can prove it. Basically a lot of sh*t is math is taken for granted, especially in recursive sets of elements, basically a function playing on itself. In short, even scientists operate on faith sometimes
basically Math is not an exact science. as black and white as math seems. its too many unknowns to know for sure of much of anything.
People reading the science and not understanding the intent of the man behind it. You got major advancements in all major sciences in the 30s and 40s, and all around his circle Godell is hearing people sh*t on religion. So in turn he took a big sh*t on their religion
What's infinity to an ant is only 6' to us as a human. A lot of times in the midst of all our progress we lose perspective, and think we run the galaxy, Godell was like:
i read it and i'm telling you it's gibberish. don't see what proving 0+1+2+3+...= (n*(n+1))/2 have to do with the summation being divergent. the whole point of the induction prove is to show that they are equal for all natural numbers. so even if infinity = n+1 or T that would still hold.
Mission249
All Star
It's part of the point, because your misunderstanding of this seems to be bleeding into your other arguments. And I don't understand how further specifying the definition refutes my argument: You asked if "1+1" is consistent and complete and I simply responded that it is not an effectively generated theory capable of expressing elementary arithmetic. So applying Godel's Incompleteness Theorem to that makes no sense.
Again, "x = x" is not an effectively generated theory capable of expressing elementary arithmetic so Godel's Incompleteness Theorem does not apply.
It only limits our human ability to conceptualize it but there are tons of mathematical facts like that. We don't go saying Euler's formula (see: http://en.wikipedia.org/wiki/Euler's_formula) is just a leap of faith because there's no physical quantification of imaginary numbers. There are some numbers that are easily expressed in base 10 that have infinitely long counterparts in base 2 and vice versa. That's just a limitation of the math tools we have and the way we perceive things.
Exactly, but the type of completeness issues we could possibly run into are not inherent in the usage of infinity. They are do to self-referential statements. E.g. "this statement is not provable" is true but not expressible in the system. This is the "Godel statement" that exists in all systems that makes Godel's theorem so amazing. I could trivial add an axiom that says "'This statement is not provable' is always true", but would that wouldn't deal with all the true statements that we can't express (i.e. incomplete) and it might lead to contradictions in other proofs (i.e. inconsistent). Note that this has nothing to do with your thoughts on infinity.
Godel's incompleteness theorem is not about "consistently and completely" proving a statement within a system. It is about an entire system not being able to be consistent, complete and effectively generated by a computer. These words, consistent and complete, have specific mathematical meanings that you seem to be mixing up with colloquial English meanings.
1) Why would you have to "assume" the base case is true when it already has its own separate, proof by induction? And if you assume anything is true then it is true and your solution has to be qualified with that assumption unless it's an implicit axiom of the system.
2) What exactly are you trying to prove? Are you trying to prove that the relation is true by making it the base case and assuming it's true?
You're clearly a smart dude but you've missed the mark on this man.
man what the f*ck @manwhatthefukk
, no, once you plug in really large numbers its wrong, that's what the (x,y) plot shows. There is no end, it goes to infinity, so in essence:0+1+...+ = (infinity*(infinity+1)/2 = (approximately) infinity*infinity/2 or infinity^2/2. Let's make subsets the of the lower and upper limit of the set to make it easier for you to understand my point.
Let's describe the upper subset (1,000,000,000=T)as {...,T,T+1,T+2}, and the lower subset as {0,1,2,3,4}. For the lower subset there's no problem. 4*(4+1)/2= 10 which is close to 4^2/2= 8. Now for the upper subset (T*(T+1))/2 = 5.000000005e17 (17 0's). T^2/2= 5e17 (17 0's). T^2 = 1e18 (18 0's). In other words, you dividing a T^2/2 = T^2-5e1. IIf it's already that little of a difference at a trillion, at infinity, the difference between n^2/2 and n^2 is truly negligible. So essentially, the bigger the number gets, the smaller the difference between n*(n+1)/2 and n^2. So once you get to really large numbers, you are saying basically that 0+1+2...+infinity+infinity+1 = infinity^2, which is why the x,y plot never approaches a finite number (aka divergent), because that's not true. Think about it man, 10*10 = 10+....+10 ten times. so how many MORE times would you have to add infinity on itself for it to equal infinity squared?
And on top of it, you are decreasing the number you are adding by each time. That would be like you expecting 10+9+8+7+...=10^2, that's crazy talk. As the axiom approaches infinity, the math behind it becomes ludicrous. You believe it's true at infinity by faith, not by fact. That is Godell's point.
Last edited:
@Mission249 , you are making me 
http://en.wikipedia.org/wiki/Gödel's_incompleteness_theorems#First_incompleteness_theorem
System of Axioms = Peano's Arithmetic
X=X thus is an axiom within the system of axioms. X=X is true for all numbers. But X=X is linear, it's not a "recursive" or "self-referential" (as you like to say) axiom/function/theorem whatever you want to call it. We are arguing about words here, you're missing the point about Godell's argument. X=X is true for all elements in the set of all natural numbers. X*(X+1)/2 is not.
You cannot see but you still believe eh? It's ok breh, I'm a believer of math as well
There are inherent in the usage of any limit based system (e.g. calculus), because any algorithm is going to have physical limitations at the limits of their calculation, thus the "error" in your calculator when the numbers are too large. Thus if the system of axioms cannot consistently calculate via the programmed algorithm, how is it consistent? You're making Godell's point unnecessarily complicated. Specifically in relation the set of all natural numbers which is the basis of all modern math, man cannot create an axiomatic system that is consistent and complete. Not technically, not physically. At some point there will be a flaw.
In mathematical terms:
Consistency:
http://en.wikipedia.org/wiki/Consistency
Let's be Mr. Smarty Pants and use the syntactic definition to avoid being "colloquial" as you like to put it. There is no system of axioms in which there does not exist a formula P that both P and its negation are provable from the axioms of the theory under its associated deductive system. Using my previous example of the algorithm {0+1+2+....}=N*(N+1)/2, Godell's example would be would be {0+...+infinity+infinity+1} = infinity*(infinity+1)/2 AND {0+...+infinity+infinity+1} /= infinity*(infinity+1)/2 are both true, which in fact they are.
Why is it that via induction the statement is true but there is a flaw in the axiom?
Breh it's too late for this sh*t, I really don't want to go back and forth on basic sh*t. Proof by Induction = YOU PROVE IT'S TRUE FOR ONE ELEMENT, THEN ASSUME IT'S TRUE FOR THE ENTIRE SET OF N, THEN YOU PROVE VIA THE INDUCTION STEP IT'S TRUE FOR N+1. THE FLAW IS IN THE WHOLE SYSTEM OF PROOF BY INDUCTION, IT REQUIRES AN ASSUMPTION!!!!
Don't worry I am still a faithful member of the church of math
http://en.wikipedia.org/wiki/Gödel's_incompleteness_theorems#First_incompleteness_theorem
System of Axioms = Peano's Arithmetic
X=X thus is an axiom within the system of axioms. X=X is true for all numbers. But X=X is linear, it's not a "recursive" or "self-referential" (as you like to say) axiom/function/theorem whatever you want to call it. We are arguing about words here, you're missing the point about Godell's argument. X=X is true for all elements in the set of all natural numbers. X*(X+1)/2 is not.
You cannot see but you still believe eh? It's ok breh, I'm a believer of math as well
There are inherent in the usage of any limit based system (e.g. calculus), because any algorithm is going to have physical limitations at the limits of their calculation, thus the "error" in your calculator when the numbers are too large. Thus if the system of axioms cannot consistently calculate via the programmed algorithm, how is it consistent? You're making Godell's point unnecessarily complicated. Specifically in relation the set of all natural numbers which is the basis of all modern math, man cannot create an axiomatic system that is consistent and complete. Not technically, not physically. At some point there will be a flaw.
In mathematical terms:
Consistency:
http://en.wikipedia.org/wiki/Consistency
Let's be Mr. Smarty Pants and use the syntactic definition to avoid being "colloquial" as you like to put it. There is no system of axioms in which there does not exist a formula P that both P and its negation are provable from the axioms of the theory under its associated deductive system. Using my previous example of the algorithm {0+1+2+....}=N*(N+1)/2, Godell's example would be would be {0+...+infinity+infinity+1} = infinity*(infinity+1)/2 AND {0+...+infinity+infinity+1} /= infinity*(infinity+1)/2 are both true, which in fact they are.
Why is it that via induction the statement is true but there is a flaw in the axiom?
Breh it's too late for this sh*t, I really don't want to go back and forth on basic sh*t. Proof by Induction = YOU PROVE IT'S TRUE FOR ONE ELEMENT, THEN ASSUME IT'S TRUE FOR THE ENTIRE SET OF N, THEN YOU PROVE VIA THE INDUCTION STEP IT'S TRUE FOR N+1. THE FLAW IS IN THE WHOLE SYSTEM OF PROOF BY INDUCTION, IT REQUIRES AN ASSUMPTION!!!! Don't worry I am still a faithful member of the church of math
Last edited: