Variation in gravity and apparent gravity[edit]
A perfect
sphere of uniform mass density, or whose density varies solely with distance from the centre (
spherical symmetry), would produce a gravitational field of uniform magnitude at all points on its
surface, always pointing directly towards the sphere's centre. The Earth is not spherically symmetric, but is slightly flatter at the poles while bulging at the Equator: an
oblate spheroid. There are consequently slight deviations in both the magnitude and direction of gravity across its surface. The
net force (or corresponding net acceleration) as measured by a scale and
plumb bob is called "effective gravity" or "apparent gravity". Effective gravity includes other factors that affect the net force. These factors vary and include things such as centrifugal force
[3] at the surface from the Earth's rotation and the gravitational pull of the Moon and Sun.
Effective gravity on the Earth's surface varies by around 0.7%, from 9.7639 m/s2 on the
Nevado Huascarán mountain in Peru to 9.8337 m/s2 at the surface of the
Arctic Ocean.
[4] In large cities, it ranges from 9.766 in
Kuala Lumpur,
Mexico City, and
Singapore to 9.825 in
Oslo and
Helsinki.
Latitude[edit]

The differences of Earth's gravity around the Antarctic continent.
The surface of the Earth is rotating, so it is
not an inertial frame of reference. At latitudes nearer the Equator, the outward
centrifugal force produced by Earth's rotation is larger than at polar latitudes. This counteracts the Earth's gravity to a small degree – up to a maximum of 0.3% at the Equator – and reduces the apparent downward acceleration of falling objects.
The second major reason for the difference in gravity at different latitudes is that the Earth's
equatorial bulge (itself also caused by centrifugal force from rotation) causes objects at the Equator to be farther from the planet's centre than objects at the poles. Because the force due to gravitational attraction between two bodies (the Earth and the object being weighed) varies inversely with the square of the distance between them, an object at the Equator experiences a weaker gravitational pull than an object at the poles.
In combination, the equatorial bulge and the effects of the surface centrifugal force due to rotation mean that sea-level effective gravity increases from about 9.780 m/s2 at the Equator to about 9.832 m/s2 at the poles, so an object will weigh about 0.5% more at the poles than at the Equator.
[3][5]
The same two factors influence the direction of the effective gravity (as determined by a
plumb line or as the perpendicular to the surface of water in a container). Anywhere on Earth away from the Equator or poles, effective gravity points not exactly toward the centre of the Earth, but rather perpendicular to the surface of the
geoid, which, due to the flattened shape of the Earth, is somewhat toward the opposite pole. About half of the deflection is due to centrifugal force, and half because the extra mass around the Equator causes a change in the direction of the true gravitational force relative to what it would be on a spherical Earth.
Altitude[edit]

The graph shows the variation in gravity relative to the height of an object
Gravity decreases with altitude as one rises above the Earth's surface because greater altitude means greater distance from the Earth's centre. All other things being equal, an increase in altitude from sea level to 9,000 metres (30,000 ft) causes a weight decrease of about 0.29%. (An additional factor affecting apparent weight is the decrease in air density at altitude, which lessens an object's buoyancy.
[6] This would increase a person's apparent weight at an altitude of 9,000 metres by about 0.08%)
It is a common misconception that astronauts in orbit are weightless because they have flown high enough to escape the Earth's gravity. In fact, at an altitude of 400 kilometres (250 mi), equivalent to a typical orbit of the
Space Shuttle, gravity is still nearly 90% as strong as at the Earth's surface. Weightlessness actually occurs because orbiting objects are in
free-fall.
[7]
The effect of ground elevation depends on the density of the ground (see
Slab correction section). A person flying at 30 000 ft above sea level over mountains will feel more gravity than someone at the same elevation but over the sea. However, a person standing on the earth's surface feels less gravity when the elevation is higher.
The following formula approximates the Earth's gravity variation with altitude:
{\displaystyle g_{h}=g_{0}\left({\frac {r_{\mathrm {e} }}{r_{\mathrm {e} }+h}}\right)^{2}}
Where
The formula treats the Earth as a perfect sphere with a radially symmetric distribution of mass; a more accurate mathematical treatment is discussed below.
Depth[edit]
See also:
Shell theorem
An approximate value for gravity at a distance r from the centre of the Earth can be obtained by assuming that the Earth's density is spherically symmetric. The gravity depends only on the mass inside the sphere of radius r. All the contributions from outside cancel out as a consequence of the
inverse-square law of gravitation. Another consequence is that the gravity is the same as if all the mass were concentrated at the centre. Thus, the gravitational acceleration at this radius is
[8]
{\displaystyle g(r)=-{\frac {GM(r)}{r^{2}}}.}
where G is the
gravitational constant and
M(
r) is the total mass enclosed within radius r. If the Earth had a constant density ρ, the mass would be
M(
r) = (4/3)π
ρr3 and the dependence of gravity on depth would be
{\displaystyle g(r)={\frac {4\pi }{3}}G\rho r.}
g at depth d is given by
g'=
g(1-
d/
R) where g is acceleration due to gravity on surface of the earth, d is depth and R is radius of
Earth. If the density decreased linearly with increasing radius from a density
ρ0 at the centre to
ρ1 at the surface, then
ρ(
r) =
ρ0 − (
ρ0 −
ρ1)
r /
re, and the dependence would be
{\displaystyle g(r)={\frac {4\pi }{3}}G\rho _{0}r-\pi G\left(\rho _{0}-\rho _{1}\right){\frac {r^{2}}{r_{\mathrm {e} }}}.}
The actual depth dependence of density and gravity, inferred from seismic travel times (see
Adams–Williamson equation), is shown in the graphs below.

Earth's radial density distribution according to the Preliminary Reference Earth Model (PREM).
[9]
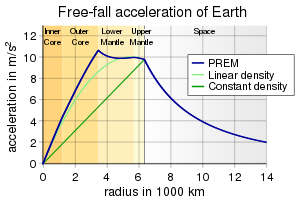
Earth's gravity according to the Preliminary Reference Earth Model (PREM).
[9] Two models for a spherically symmetric Earth are included for comparison. The dark green straight line is for a constant density equal to the Earth's average density. The light green curved line is for a density that decreases linearly from centre to surface. The density at the centre is the same as in the PREM, but the surface density is chosen so that the mass of the sphere equals the mass of the real Earth.
Local topography and geology[edit]
See also:
Physical geodesy
Local differences in
topography (such as the presence of mountains),
geology (such as the density of rocks in the vicinity), and deeper
tectonic structure cause local and regional differences in the Earth's gravitational field, known as
gravitational anomalies.
[10] Some of these anomalies can be very extensive, resulting in bulges in
sea level, and throwing
pendulum clocks out of synchronisation.
The study of these anomalies forms the basis of gravitational
geophysics. The fluctuations are measured with highly sensitive
gravimeters, the effect of topography and other known factors is subtracted, and from the resulting data conclusions are drawn. Such techniques are now used by
prospectors to find
oil and
mineral deposits. Denser rocks (often containing mineral
ores) cause higher than normal local gravitational fields on the Earth's surface. Less dense
sedimentary rocks cause the opposite.
Other factors[edit]
In air, objects experience a supporting
buoyancy force which reduces the apparent strength of gravity (as measured by an object's weight). The magnitude of the effect depends on air density (and hence air pressure); see
Apparent weight for details.
The gravitational effects of the
Moon and the
Sun (also the cause of the
tides) have a very small effect on the apparent strength of Earth's gravity, depending on their relative positions; typical variations are 2 µm/s2 (0.2
mGal) over the course of a day.









